大学生创新训练项目申请书
项目编号 s201910536007
项目名称
如果您无法在线浏览此 PDF 文件,则可以
下载免费小巧的 福昕(Foxit) PDF 阅读器,安装后即可在线浏览 或
下载免费的 Adobe Reader PDF 阅读器,安装后即可在线浏览 或
下载此 PDF 文件
如果您无法在线浏览此 PDF 文件,则可以
下载免费小巧的 福昕(Foxit) PDF 阅读器,安装后即可在线浏览 或
下载免费的 Adobe Reader PDF 阅读器,安装后即可在线浏览 或
下载此 PDF 文件
项目负责人 王涛 联系电话 17307402108
所在学院 土木工程学院
学 号 201608020632 专业班级 土木工程(城轨)1601
指导教师 彭涛
E-mail 3487889498@qq.com
申请日期 2019年4月30日
起止年月 2019年 05月至 2021年05月
37000vip威尼斯
填 写 说 明
1、本申请书所列各项内容均须实事求是,认真填写,表达明确严谨,简明扼要
2、申请人可以是个人,也可为创新团队,首页只填负责人。“项目编号”一栏不填。
3、本申请书为大16开本(A4),左侧装订成册。可网上下载、自行复印或加页,但格式、内容、大小均须与原件一致。
4、负责人所在学院认真审核, 经初评和答辩,签署意见后,将申请书(一式两份)报送××××大学项目管理办公室。
一、
基本情况
项目
名称
|
基于频率法的刚性吊杆拉力测试实验研究
|
所属
学科
|
学科一级门:
|
工学
|
学科二级类:
|
土木类
|
申请
金额
|
20000 元
|
起止年月
|
2019年 05月至 2021年05月
|
负责人
姓名
|
王涛
|
性别
|
男
|
民族
|
汉
|
出生年月
|
1998年 08月
|
学号
|
201608020632
|
联系
电话
|
宅:17307402108 手机: 17307402108
|
指导
教师
|
彭涛
|
联系
电话
|
宅:13378918186 手机: 13378918186
|
负责人曾经参与科研的情况
|
项目负责人王涛学习努力,成绩优异,勤于思考,乐于科研,每年都获得学校奖学金;拥有较好的数学、力学基础,动手能力较强,积极参加各项科研和竞赛活动,获得过“第十四届湖南省大学生力学竞赛”一等奖;前期对基于频率法的吊杆拉力测试理论与实验方面都进行了较充分的准备。
|
指导教师承担科研课题情况
|
彭涛老师一直从事桥梁结构设计与仿真分析、桥梁结构检测与健康监测、桥梁施工控制等方面的教学和科研工作,参加过国家自然科学基金和湖南省科技重大专项等多个纵向科研项目,作为技术负责人参与多个重大桥梁工程的科研工作,获湖南省2011年度科技进步一等奖(排名第4)。
|
指导教师对本项目的支持情况
|
指导教师前期参加过多座大桥的吊杆拉力测试,对一般索、梁结构的振动特性和模态参数识别方面有较丰富的经验;前期对东平大桥不同长细比的刚性吊杆进行了振动测试,为项目研究积累了大量实测数据;指导老师在理论分析、数值仿真和实验测试方面都能够为本项目提供支持。
|
项
目
组
主
要
成
员
|
姓 名
|
学号
|
专业班级
|
所在学院
|
项目中的分工
|
蒋林
|
201608020306
|
城轨1601
|
土木工程学院
|
实验测试
|
兰川云
|
201608020603
|
城轨1601
|
土木工程学院
|
理论分析,数值仿真
|
张苗
|
201608020601
|
城轨1601
|
土木工程学院
|
实验测试
|
李淼
|
201608020405
|
城轨1602
|
土木工程学院
|
理论分析,数值仿真
|
二、 立项依据(可加页)
(一) 项目简介
刚性吊杆作为一种常用吊杆形式,近年来在钢拱桥中得到广泛应用。现有的频率法测拉力的理论基础是基于弦振动理论,由于忽略了抗弯刚度和剪切变形等因素的影响,该法目前不适用于刚性吊杆的拉力测试。本项目拟开展刚性吊杆拉力测试实验研究,建立能够考虑抗弯刚度、各种边界条件和剪切变形等影响的刚性吊杆拉力与频率之间的精确对应关系,以期得到刚性吊杆拉力测试的适用计算方法,通过频率测试准确、高效的识别出刚性吊杆的拉力。
(二) 研究目的
刚性吊杆作为一种常用吊杆形式,近年来在大跨度钢箱拱和钢桁架拱桥中得到广泛应用,国内采用刚性吊杆的典型拱桥有佛山东平大桥、重庆宜万铁路万州长江大桥、南京大胜关长江大桥、江西九江长江大桥(见图1)等。与采用高强度钢丝或钢绞线的柔性吊杆结构相比,刚性吊杆的几何、物理特性有明显的差别,刚性吊杆的线密度、轴向和弯曲刚度较大;刚性吊杆边界条件复杂,且振动频率对边界条件非常敏感;而且由于抗风的需要,刚性吊杆上一般都留有抗风的孔洞。这就决定了刚性吊杆的动力学特性与柔性吊杆结构有着显著的差异。
|
|

(a)佛山东平大桥
|

(b)重庆宜万铁路万州长江大桥
|

(c)南京大胜关长江大桥
|

(d)江西九江长江大桥
|
图1 国内几座采用刚性吊杆的典型拱桥
频率法测拉力是目前吊杆拉力测定中应用最广泛的方法,其原理是首先通过振动测试,识别出索的自振频率,由于拉力与其振动频率之间存在着特定的关系,拉力可由频率换算而间接得到。现有的频率法测拉力的理论基础是基于弦振动理论,常将拉索或吊杆理想化为张紧的弦,但是由于忽略了抗弯刚度和剪切变形等因素的影响,现有的频率法很难适用于刚性吊杆的拉力测试。因此,开展刚性吊杆拉力测试实验研究,建立能够考虑刚性吊杆抗弯刚度及其单位长度质量、复杂边界条件、剪切变形、吊杆孔洞影响的刚性吊杆拉力与频率之间的精确对应关系,由此得出适用于刚性吊杆拉力测试的计算公式,解决刚性吊杆拉力测试的难题。
(三) 研究内容
基于前期研究的积累,申请者将本次项目研究的主要内容分为两个部分:理论机理研究与实验研究。
理论机理研究:
①针对刚性吊杆的振动特点,分别从Euler-Bernoulli梁和Timoshenko梁理论出发,建立刚性吊杆的振动微分方程,并进行理论推导和求解得到频率和拉力之间的实用计算公式或编制程序进行数值求解;
②分析不同长细比的刚性吊杆的抗弯刚度、附加质量、剪切变形对拉力测试结果的影响;
③运用有限元法,建立刚性吊杆的实体或板壳模型,得到吊杆振动频率和拉力间的对应关系,并与解析法得到的结果和实验结果进行对比分析,研究不同长细比条件下,各计算公式的精度与适用范围。
实验研究:
①分别制作三组不同长细比的腹板开孔和不开孔的H型刚性吊杆(吊杆横截面相同,三组刚性吊杆长度分别为2m、3.5m、5m,初步拟定的刚性吊杆截面如图2所示);
②通过开发的实验装置,分别对各刚性吊杆进行两级加载,并利用振动测试系统对其空载和加载状态下的振动特性进行测试,得到实测振动频率,实验装置如图2所示;
③利用实验系统中的压力传感器测得的力值加上实测的部分实验装置自重,得到刚性吊杆上的实测拉力值,并利用百分表测得的位移对实测拉力值进行校核和验证。
④对实测和理论计算数据进行对比分析,研究不同长细比条件下,各计算公式的精度与适用范围。
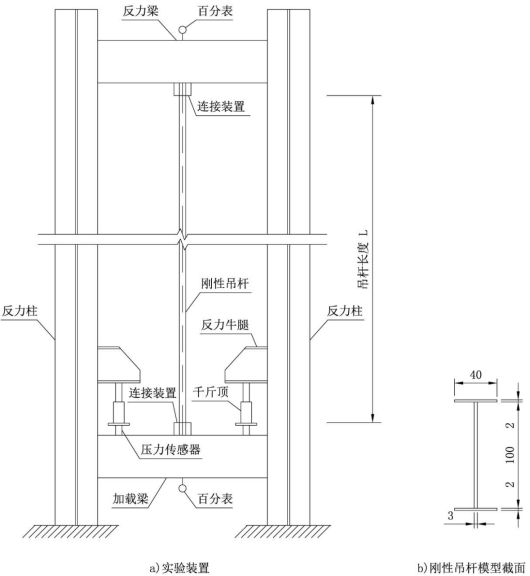
图2 实验装置和刚性吊杆模型截面示意图(单位:mm)
(四) 国、内外研究现状和发展动态
目前,国内外常用的吊杆索力(或拉力)测试方法主要有压力传感器法、液压千斤顶法、频率法、磁通量法、量测应变法等几种。
(1)压力传感器法。该法是将压力传感器安装在吊杆的锚固端或张拉端,通过传感器感应锚头的压力来测量索的拉力。这种方法适用于在施工过程中预先埋设了传感器的吊杆。从理论上讲,压力传感器法精度较高,但是,由于测试的每根吊杆下都要一次性埋设传感器,成本较高。而且该方法只适合于柔性吊杆,难以应用于刚性吊杆。
(2)液压千斤顶法。该法是利用千斤顶的张拉油缸中的读数和张拉力的关系,通过测得精密压力表或液压传感器测定油缸的液压读数,就可求得张力。这种方法简单易行,是施工中测试索力最实用的方法。但是这种方法只适用于施工阶段索力的测试,不适用于成桥以后的索力测试,一般在工程中只是作为监测索力的辅助手段。且该法只适合于需要张拉的柔性索或吊杆,不适合于不需要张拉的刚性吊杆。
(3)频率法。该法是根据吊杆拉力和振动频率之间的关系求得索力。通常用精密的拾振器,以环境振动或者强迫激励吊杆,传感器记录下时程数据,经过滤波、放大和频谱分析,根据频谱图得到索的振动频率,再利用拉索张拉力与自振频率之间的关系算得索力。这种测试方法只要测得拉索或吊杆的各阶振动频率,经过简单计算便可以得到索力,且设备可重复使用,因此频率法是目前应用最为广泛的一种索力测试技术。
(4)磁通量法。该法是一种新颖的索力测试方法,它利用放在索中的小型电磁传感器,测定磁通量变化,根据索力、温度与磁通量变化的关系,推算索力。当拉索材料中的应力发生变化时,磁滞曲线也发生变化,测定磁通量渗透系数就可以推算出拉索的应力,从而容易推算得到拉索的索力。这种测试方法中磁通量法技术目前国外应用比较多,但在国内尚未成熟,几乎不见使用。
(5)量测应变法。该法是将应变片粘贴在敏感元件上,然后把敏感元件粘贴到被测吊杆的表面,载荷通过对表面的作用传递到应变片上,然后根据应变值推算吊杆拉力。虽然该方法原理简单,但测量索力(或拉力)时不可靠。
上述几种方法中,前两种方法适用于张拉施工阶段,而后三种方法可用于施工及使用阶段的索力测试。频率法不仅具有测试仪器日趋小型化、携带方便、容易安装、可以重复使用、测试效率高的优点,而且其测试精度高,因此频率法是目前应用最为广泛而有效的一种吊杆索力或拉力测试方法。
早在20世纪70年代初期,Irvine H M就在英国伦敦的会议上发表了关于索的自由振动理论[1],并于80年代初期就对索的动力学理论撰写了专著[2],为建立索振动理论体系奠定了基础。1988年,日本Shimada等人通过实验的方法研究弯曲刚度对拉索张力识别的影响[3]。1994年,Shimada等提出了利用高阶频率识别索力的方法,通过考虑弯曲刚度、垂度等因素的影响求解准确的拉索索力[4]。1996年,日本学者Hiroshi Zui等提出了基于频率法考虑弯曲刚度和垂度的经验公式,只要测得拉索的前两阶振型的频率,便可以利用经验公式求解拉索的索力[5]。1998年,美国Russell和Lardner通过大量实验证明各阶频率之间不会发生相互交叉。同时,基于实测频率与理论频率之间的比较分析,Russell和Lardner提出了新的索力识别的方法[6]。美国Mehrabi等引入无量纲参数,考虑了弯曲刚度、边界约束等影响因素,利用有限差分法,通过特征值计算得到索力,并与有限元计算结果比较,该方法具有较高精度[7]。同年,日本Yamagiwa等分析了考虑两端铰接与两端固结对索力计算带来的区别,提出利用拉索上两个测点的振动响应关系推算吊杆张力和刚度[8]。2002年,日本Zui H等提出用Kalman滤波方法并根据激振锤等外界条件引起的振动识别吊杆的弯曲刚度和张力,并给出了带有附加质量块的拉索自振频率的详细解析解[9]。2005年,美国Roman等注意到实测中拉索高阶频率比理想张拉弦偏高的现象,采用适用的理论公式识别拉索的抗弯刚度以及索力[10]。2007年,韩国Byeong H K等提出了基于频率的灵敏度修正识别系统,可以同时识别索力、弯曲刚度及轴向刚度,并通过有限元模型分析验证了可行性[11]。
我国对频率法的研究起步相对较晚,但随着相关研究的展开和深入,在提高频率法测试索力精度方面也逐步积累了经验和取得了一定的成效。1995年,郭良友对绳、索振动的特征进行理论分析,并从理论上分析了弯曲刚度对绳、索频率和索力的影响[12]。1997年,方志、张智勇在用频率法测试斜拉桥索力时,分别用有限元法和解析法分析了索的刚度、垂度、边界条件等因素对频率法测试结果精度的影响[13]。1999年,蔡敏等[14]提出温度、雨,雪以及风等环境因素对索的基频都有一定的影响。2001年,吴海军等忽略索的抗弯刚度影响,推导得出索的张力与索固有频率的平方成正比的关系[15]。同年,宋一凡、贺拴海根据拉索振动特点,引入动力计算长度概念,将两端固结的拉索振动模型动力等效成两端铰结的拉索振动模型[16];王卫锋、韩大建基于拉索振动模型,分析了拉索的刚度、垂度、边界条件对频率法测试精度的影响[17]。2002年,侯俊明等研究了日照温度变化对索力值的影响规律[18]。2003年,刘文峰等在假定边界条件为简支以及简支和固支耦合的情况下考虑索的刚度,得到了不同假设条件下的理论公式,讨论了不同方法下索力的区别,并利用实测数据进行分析[19]。2004年,魏建东利用非线性有限元法程序,对拉索频率和索力之间的关系进行了参数分析,并比较了各种索力测试公式的计算精度[20];邵旭东等利用能量法,引入固端梁在均布荷载下的挠度曲线作为一阶振型,求得吊索的一阶频率与抗弯刚度、张力的近似关系,建立微分方程,通过求解分别得到两端铰结吊索和弦的一阶频率与抗弯刚度、张力的精确关系[21]。2005年,任伟新、陈刚也基于弦振动理论,采用能量法和曲线拟合的方法,建立了分别考虑垂度和抗弯刚度影响的计算公式[22];郑罡等基于较完善的有限元模型,通过最小化频率测量值与计算值间的误差,建立了利用多阶测试频率识别斜拉索张力、长度、抗弯刚度、等多个参数的基本理论,提高了斜拉索张力测试的准确性[23];苏成等通过有限元法及样条拟合技术获取斜拉索索力与频率的对应关系,并提出了基于多阶频率识别斜拉索抗弯刚度的方法[24]。2006年,周云等在斜拉索截面信息未知的情况下,利用一种实用的拟合方法得到了拉索的刚度[25]。2007年,吴文清等提出用索力标定的方法识别索的力学参数[26];陈淮通过引入参数简化吊索张力与基频的关系,采用数值计算和曲线拟合的方法推导出了考虑吊索弯曲刚度和两端边界条件的张力实用计算公式[27]。2008年,赵跃宇等研究了斜拉索弯曲刚度对面内、面外的一阶及高阶固有频率的影响,并分析了斜拉索长度和初张力等参数对固有频率的影响[28]。2011年,陈彦江等[29]以吊杆的索力值、抗弯刚度和计算长度作为未知参数,分析吊杆频率对各参数的敏感程度,提出了一种基于参数灵敏度的迭代算法的吊杆索力识别方法。2018年,韩州斌等[30]分析了平行钢绞线索的离散性、垂度和区域性接触对索力测试的影响,采用振动法对杭埠河大桥平行钢绞线索进行了索力测试。
迄今为止,国内外学者对频率法的研究基本上都是采用均匀拉索(均匀拉索是指两锚固点之间索段的横截面为等截面、材质均匀、材料的应力应变符合虎克定律的拉索)的振动模型,测试的对象都是斜拉桥拉索、悬索桥吊杆、拱桥吊杆等柔性索结构,尚未见到采用频率法测试刚性吊杆拉力的报道。与柔性索结构相比,刚性吊杆的几何、物理特性有明显的差别,刚性吊杆的线密度、轴向和弯曲刚度较大;刚性吊杆边界条件复杂,且振动频率对边界条件非常敏感;而且由于抗风的需要,刚性吊杆上一般都留有抗风的孔洞。这就决定了刚性吊杆的动力学特性与柔性索结构有着显著的差异,因此,现有的频率法很难适用于刚性吊杆的拉力测试,考虑刚性吊杆抗弯刚度及其单位长度质量、复杂边界条件、吊杆孔洞影响,建立适合刚性吊杆拉力测试的拉力、频率之间的精确对应关系具有重要的理论和工程现实意义。
参考文献:
[1] Irvine H M.and T.K.Cauchy.The linear theory of free vibration of a suspended cable.Proceeding of the Royal.Society,London,England.Series A,V01.341.1974.
[2] Irvine HM.Cable Structures[M].Cambridge:MrI’Press,1981
[3] Shimada T, Nishimura A.Effect of flexural rigidity on cable tension estimated by vibration method.土木学会论文集.1988,10.No.398/I-10,409-412.
[4] Shimada T, Estimating method of cable tension from natural frequency of high mode, 土木学会论文集.1994,No.501/I-29,163-171.
[5] Zui H,Shinke T,Nan’tim Y.Practical formulas for estimation of cable tension by vibration method[J].Journal of Structural Engineering,ASCE,1 996,122(6):651-656
[6] Russell J.C.and Lardner.T.J.Experimental determination of frequencies and tension for elastic cables.J.Struct.Eng.,1998, 124_10,1067-1072.
[7] Mehrabi, A., and Tabatabai, Unified finite difference formulation for free vibration of cables.J.Struct.Eng., 124_11,1313-1322-1998.
[8] Yamagiwa I., Utsuno H,Sugii K,et a1., Simultaneous identification of tension and flexural rigidity of cables,Kobe steel engineering reports,1999,49(2):12-15.
[9] Zui H,Hamazaki Y, Namita Y, Study on tension and flexural rigidity identification for cables having large ratio of the diameter and the length,Journal of structural mechanics and earthquake engineering,JSCE.2002,No.703/I-59,141-149.
[10] Roman Geier, Guido De Roeck, Johannes Petz. Cable force determination for the Danube channel bridge in Vienna[J].Structural Engineering International.2005,l5(3):181-185.
[11] Byeong Hwa Kim, Taehyo Park.Estimation of cable tension force using the frequency-based system identification method[J].Journal of sound and vibration 2007,304:660-676.
[12] 郭良友.绳、索的振动特性及斜拉索的索力测量[J].桥梁建设.1995,1:61-64.
[13] 方志,张智勇.斜拉索的索力测试[J].中国公路学报.1997,10(1):51-58.
[14] 蔡敏,蔡键,李彬等.环境因素对斜拉桥斜索自振频率的影响[J].合肥工业大学学报(自然科学版).1999,22(5):36-39.
[15] 吴海军,陈思甜,龚尚龙等.斜拉桥索力测试方法研究[J].重庆交通学院学报.2001,20(4):23-25.
[16] 宋一凡,贺拴海.斜拉索动力计算长度研究[J].中国公路学报.2001.14(3):70-72.
[17] 王卫锋,韩大建.斜拉桥的索力测试及其参数识别川.华南理工大学学报(自然科学版).2001,29(1):18-21.
[18] 侯俊明,彭晓彬,叶力才.斜拉索索力的温度敏感性[J].长安大学学报:自科学版.2002.22(4):34-36.
[19] 刘文峰,应怀樵,柳春图.考虑刚度及边界条件的索力精确求解[J].振动与冲
击.2003.22(4):12-14.
[20] 魏建东.索力测定常用公式精度分析[J].公路交通科技.2004,21(2):53-56.
[21] 邵旭东,李国峰,李立峰.吊索振动分析与力的测量[J].中外公路.2004,24(6):29-31.
[22] 任伟新,陈刚.由基频计算拉索拉力的实用公式[J].土木工程学报.2005,38(11):26-31.
[23] 郑罡,倪一清,高赞明等.斜拉索张力测试和参数评估的理论和应用[J].土木工程学报.2005,38(3):64-69
[24] 苏成,徐郁峰,韩大建.频率法测量索力中的参数分析与索抗弯刚度的识别[J].公路交通科技.2005,22(5):75-78.
[25] 周云,易伟建.斜拉索截面信息未知时的刚度识别及索力计算[J].湖南农业大学学报(自然科学版).2006,32(4):445-449.
[26] 吴文清,王成树,刘国昌等.大跨度系杆拱桥柔性吊杆张力监测和参数识别研究.公路交通科技.2007,24(1):69-73.
[27] 陈淮,董建华.中、下承式拱桥吊索张力测定的振动法实用公式[J].中国公路学报.2007,20(3):66-70.
[28] 赵跃宇,周海兵,金波等.弯曲刚度对斜拉索非线性固有频率的影响[J].工程力学.2008,25(1):196-202.
[29] 陈彦江,程建旗,闫维明,何浩祥,李勇.基于参数灵敏度分析的吊杆索力识别[J].振动与冲击,2011,30(07):256-260.
[30] 韩州斌,李东升,杨洋.等值张拉时基于振动法的平行钢绞线索索力测试分析[J].公路交通科技,2018,35(02):55-61.
(五) 创新点与项目特色
1、目前,国内外文献尚未见利用频率法测试刚性吊杆拉力的报道,本实验展开这方面的研究在吊杆拉力测试中是一个创新,在频率法的应用上也是一个较为合理的新思路,具有显著的特色。
2、拟分别从Euler-Bernoulli梁和Timoshenko梁理论出发,建立刚性吊杆的振动微分方程,并进行相关理论和数值求解,通过实验研究得到通过实测吊杆振动频率获得拉力值的方法,这与现有的用于柔性吊杆拉力测试的频率法相比,由于理论基础不同,研究工作将具有较大的创新性。
(六) 技术路线、拟解决的问题及预期成果
技术路线
(1)继续收集国内外涉及拉索、吊杆振动机理研究,拉索、吊杆拉力测试及识别等方面的最新文献资料,进一步拓宽研究思路;选择适当的理论,对后续实验可能出现的各种情况进行预先理论机理研究。
(2)分别制作三组不同长细比的腹板开孔和不开孔的H型刚性吊杆(吊杆横截面相同,三组刚性吊杆长度分别为2m、3.5m、5m)。
(3)通过开发的实验装置,分别对各刚性吊杆进行两级加载,并利用振动测试系统对其空载和加载状态下的振动特性进行测试,得到实测振动频率。
(4)利用实验系统中的压力传感器测得的力值加上实测的部分实验装置自重,得到刚性吊杆上的实测拉力值,并利用百分表测得的位移对实测拉力值进行校核和验证。
(5)从Euler-Bernoulli梁和Timoshenko梁理论出发,建立刚性吊杆的振动微分方程,并进行理论推导和数值求解,得到频率和拉力之间的理论计算公式或编制数值求解程序。
(6)建立刚性吊杆的实体或板壳有限元模型,从有限元分析角度对解析法进行验证,以期通过实验得到刚性吊杆索力测试的适用计算方法,通过频率法,准确高效的识别出刚性吊杆的拉力。
(7)对实测和理论计算数据进行对比分析,研究不同长细比条件下,各计算公式的精度与适用范围,不断修正理论,最后提出一种实用的基于频率法的刚性吊杆拉力测试方法。
预期成果
(1)从刚性吊杆振动特性出发,通过实验研究,得到基于频率法的刚性吊杆拉力测试方法,并通过有限元法对该方法进行验证,解决不同长细比刚性吊杆拉力测试的难题。
(2)依靠本项目的研究预期发表1~2篇学术论文。
(七) 项目研究进度安排
该项目的预期研究时限为两年:
(1)2019年5月至2020年4月:参考各个渠道的论文以及书籍,完善本次研究的理论体系,规划好实验步骤,准备好实验过程中所需要的各种装置和模型;从Euler-Bernoulli梁和Timoshenko梁理论出发,建立刚性吊杆的振动微分方程,并进行相应的理论推导和数值求解;分析不同长细比的刚性吊杆的抗弯刚度、附加质量、剪切变形对拉力测试结果的影响;按理论分析结果进行实验,测试各实验工况下刚性吊杆的自振频率,并利用实验系统中的压力传感器测得的力值加上实测的部分实验装置自重,得到刚性吊杆上的实测拉力值,并利用百分表测得的位移对实测拉力值进行校核和验证。
(2)2020年5月-2021年5月:运用有限元法,建立刚性吊杆的实体或板壳模型,得到吊杆振动频率和拉力间的对应关系,并与解析法和实验得到的结果进行对比,分别从有限元法和实验实测两个方面对上述研究进行验证,验证前一阶段得出的结论是否正确,并对其进行修正。最后,把关于本次研究的全部内容进行整理,再次探讨,确定最终结论,提交研究报告等结题材料,正式结题。
(八) 已有基础
1. 与本项目有关的研究积累和已取得的成绩
(1)本项目研究方向是土木工程研究热点问题,涉及桥梁检测和结构健康监测等方向,具有重要研究意义。项目组成员已基本完成大学本科基础课与专业基础课程的学习,对土木工程专业方向的科学研究与创新训练具有浓厚的兴趣,团队成员动手能力强,且具有独立思考与解决问题的能力,能够胜任本项目的研究任务。
(2)指导老师前期参加过多座大桥的索力或拉力测试,对基于频率法的柔性、刚性吊杆拉力测试有深刻的认识,对一般索、梁结构的振动特性和模态参数识别方面有较为丰富的经验;作为技术负责人参与了采用刚性吊杆的东平大桥的施工控制和成桥荷载试验研究工作,在大桥的施工期和成桥后,对刚性吊杆进行了多次振动测试,具有不同长细比刚性吊杆振动测试的第一手资料,为项目研究提供了大量的实测数据;此外,指导老师精通桥梁工程常用的有限元分析软件,能指导学生准确、高效的建立大型有限元模型对结构进行静动力分析。
2. 已具备的条件,尚缺少的条件及解决方法
(1)已具备的条件
本项目依托单位37000vip威尼斯拥有设备先进的结构实验中心,为湖南省工程实验室和湖南省工程研究中心;且拥有省部共建(桥梁工程安全控制)教育部重点实验室,占地面积3500平方米,拥有总价值3000万元仪器设备,设备齐全,具备了开展本项目研究所需要的各项试验条件,并能得到拥有丰富实验测试经验的老师指导,与本项目相关的主要试验设备与装置如下:
① FCS 电液伺服加载系统;
② 多台索力动测仪、振动及动态数据采集分析系统、力和应变数据采集分析系统、位移测试系统;
③ 油压张拉设备;
④ ANSYS、MIDAS等分析软件。
(2)尚缺少的条件及解决方法
尚缺少刚性吊杆模型与加载连接装置,拟通过采购相关钢结构和附件材料加工制作后获得。